Установление взаимосвязей между явлениями — одна из основных задач статистического анализа. На это есть две причины. Первый. Если известно, что один процесс зависит от другого, то на первый можно повлиять через последний. В соответствии с. Даже при отсутствии причинно-следственной связи изменение одного показателя может предсказать изменение другого.
Связь между двумя переменными проявляется в совместной вариации: при изменении одного показателя появляется тенденция к изменению и другого. Эта взаимосвязь называется корреляцией, а раздел статистики, посвященный взаимосвязям, называется корреляционным анализом.
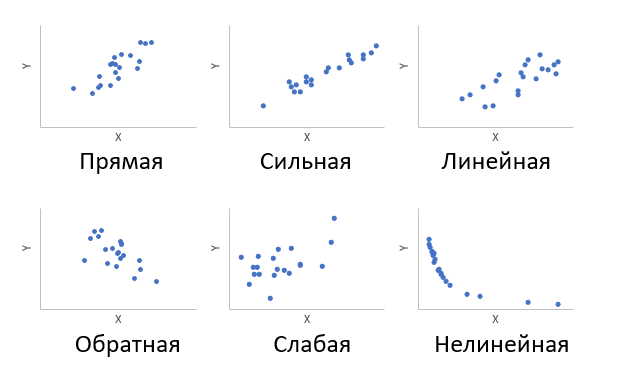
Корреляция, попросту говоря, взаимосвязанное изменение показателей. Он характеризуется направлением, формой и уплотнением. Примеры корреляций показаны ниже.
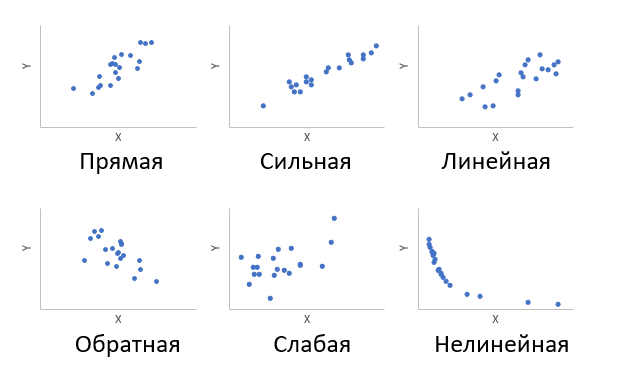
Кроме того, будет рассматриваться только линейная корреляция. График разброса (график корреляции) показывает взаимосвязь двух переменных X и Y. Пунктирными линиями показаны средние значения.
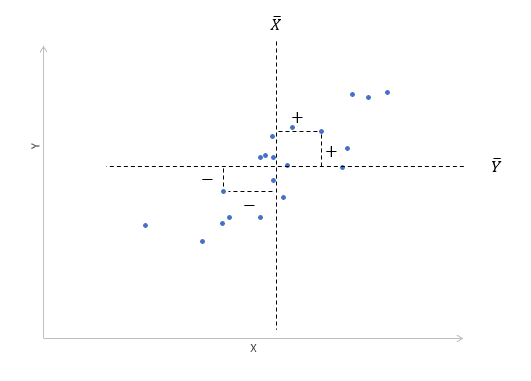
При положительном отклонении X от среднего значения Y также отклоняется в положительном направлении от своего среднего значения в большинстве случаев. Поскольку X ниже среднего, Y также обычно ниже среднего. Это прямая или положительная корреляция. Существует обратная или отрицательная корреляция, когда положительное отклонение от среднего значения X связано с отрицательным отклонением от среднего значения Y, или наоборот.
Линейность корреляции проявляется в том, что точки лежат на одной прямой. Положительный или отрицательный наклон этой линии определяется направлением отношения.
Чрезвычайно важная особенность корреляции — ее теснота. Чем плотнее связь, тем ближе к точке прямой линии на схеме. Как это можно измерить?
Нет смысла складывать отклонения каждого показателя от его среднего, получаем ноль. Аналогичная проблема возникла при измерении вариации, а точнее, дисперсии. Там эту проблему можно обойти, возводя каждое отклонение в квадрат.
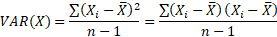
Квадрат отклонения от среднего измеряет отклонение индикатора как бы относительно самого себя. Если второй фактор числителя заменить отклонением от среднего значения второго показателя, получается совместная вариация двух переменных, которая называется ковариацией.
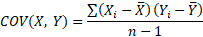
Чем больше пар имеют одинаковый знак отклонения от среднего, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация указывает на прямую связь между переменными. Обратная связь дает отрицательную ковариацию. Если количество совпадающих отклонений в знаке примерно равно количеству несовпадающих, ковариация стремится к нулю, что свидетельствует об отсутствии линейной зависимости.
Следовательно, чем выше модуль ковариации, тем теснее линейная зависимость. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнить корреляции для разных переменных. Определить направление можно только по знаку. Чтобы получить стандартизованное значение близости отношения, необходимо исключить единицы измерения, разделив ковариацию на произведение стандартных отклонений обеих переменных. В результате вы получите формулу коэффициента корреляции Пирсона.
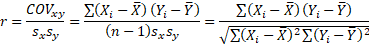
Индикатор имеет полное название коэффициент линейной корреляции Пирсона или просто коэффициент корреляции.
Коэффициент корреляции показывает близость линейной зависимости и колеблется от -1 до 1. -1 (минус один) указывает на полную (функциональную) линейную обратную зависимость. 1 (один) — полная линейная положительная связь (функциональная). 0 — нет линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже приведены несколько примеров с разными значениями коэффициента корреляции.
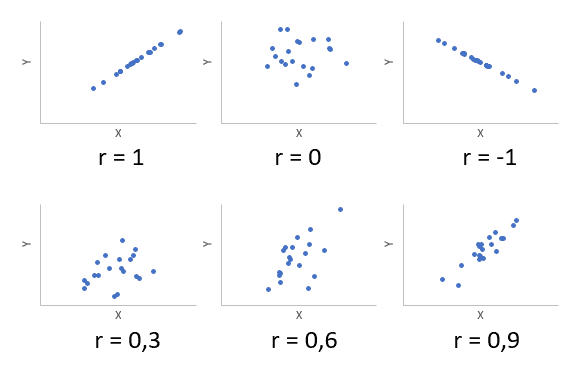
Следовательно, ковариация и корреляция отражают жесткость линейной зависимости. Последний используется гораздо чаще, поскольку является относительным показателем и не имеет единицы измерения.
Диаграммы разброса дают визуальное представление о том, что измеряет коэффициент корреляции. Однако требуется более формальная интерпретация. Эту роль играет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации и обычно используется для оценки качества регрессионных моделей. Представьте снова линию, вокруг которой лежат точки.
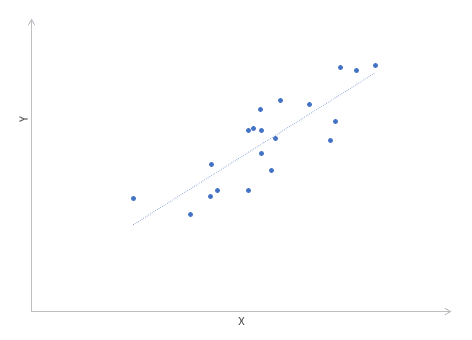
Линейная функция представляет собой модель взаимосвязи между X и Y и показывает ожидаемое значение Y для данного X. Коэффициент детерминации — это отношение дисперсии ожидаемого Y (точки на линии) к общей дисперсии Y , или пропорция объясненной вариации Y. Для r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывается по выборке. Это означает, что аналитик имеет в своем распоряжении не истинный смысл, а оценку, которая всегда ошибочна. Если выборка была репрезентативной, истинное значение коэффициента корреляции относительно близко к оценке. В какой степени можно определить с помощью доверительных интервалов.
Согласно центральной предельной теореме, распределение оценки любого показателя имеет тенденцию к нормализации по мере роста выборки. Но есть проблема. Распределение коэффициента корреляции вблизи предельных значений несимметрично. Ниже приведен пример распределения с истинным коэффициентом корреляции ρ = 0,86.
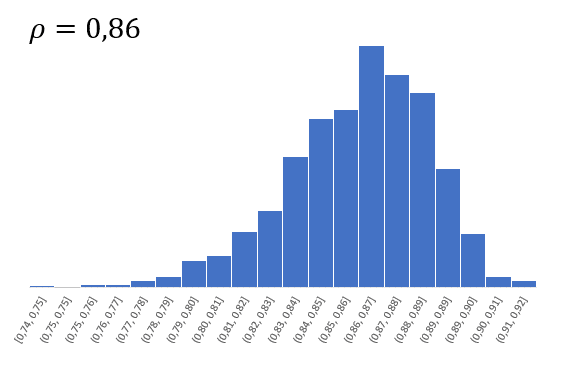
Предельное значение не позволяет выйти за пределы 1 и как бы «раздавит» распределение вправо. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем случае нельзя полагаться на свойства нормального распределения. Поэтому Фишер предложил преобразовать выборочный коэффициент корреляции по формуле:

Распределение z для того же r выглядит следующим образом.
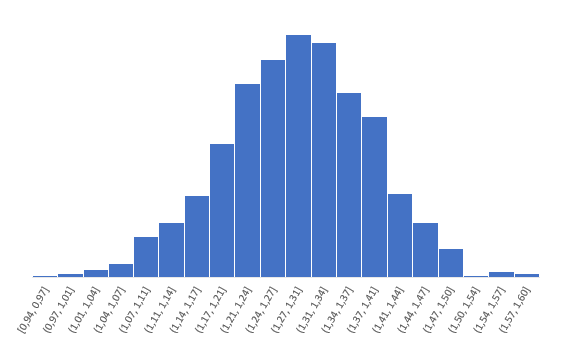
Намного ближе к нормальному. Стандартная ошибка z:
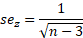
Кроме того, исходя из свойств нормального распределения, легко найти верхнюю и нижнюю границы доверительного интервала для z. Мы определяем квантиль стандартного нормального распределения для данного уровня достоверности, то есть количество стандартных отклонений от центра распределения.
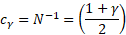
cγ — квантиль стандартного нормального распределения;
N-1 — стандартная обратная функция распределения;
— уровень достоверности (часто 95%).
Затем рассчитываем границы доверительного интервала.
Нижний предел z:
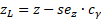
Верхний предел z:
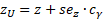
Теперь с помощью обратного преобразования Фишера от z мы вернемся к r.
Нижний предел r:
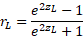
Верхний предел r:
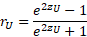
Это была теоретическая часть. Перейдем к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше всего начинать с визуализации.
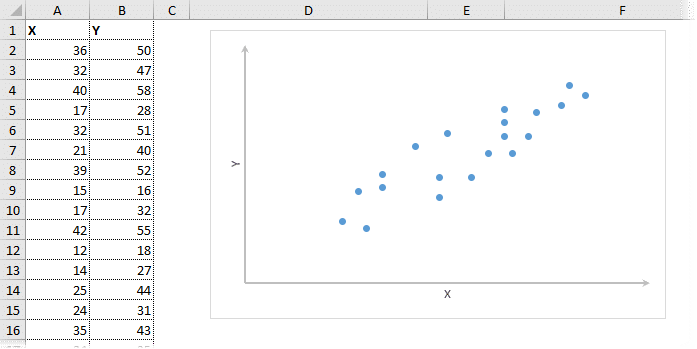
На диаграмме показана взаимосвязь двух переменных. Мы рассчитываем коэффициент корреляции пар с помощью функции КОРРЕЛЬ в Excel. В аргументах необходимо указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это всего лишь оценка, поэтому перейдем к оценке диапазона.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Excel нет готовых функций для расчета доверительного интервала коэффициента корреляции, например для среднего арифметического. Поэтому план такой:
— Выполните преобразование Фишера для r.
— На основе нормальной модели рассчитайте доверительный интервал для z.
— Выполните обратное преобразование Фишера от z до r.
Удивительно, но есть специальная функция FISHER для преобразования Fisher в Excel.
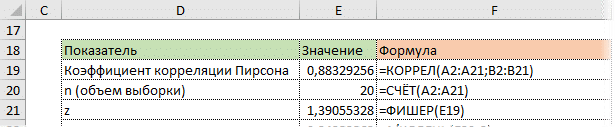
Стандартная ошибка z легко вычисляется по формуле.
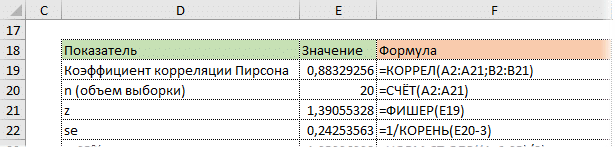
Используя функцию NORM.ST.OBR, определите квантиль нормального распределения. Возьмем уровень уверенности 95%.
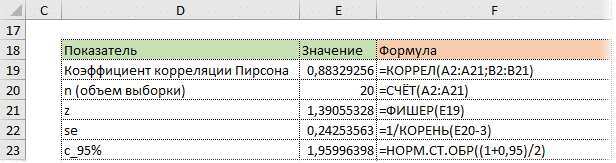
Значение 1,96 хорошо известно любому опытному аналитику. 95% нормально распределенных значений находятся в пределах ± 1,96σ от среднего.
Используя z, стандартную ошибку и квантиль, мы можем легко определить доверительные границы для z.
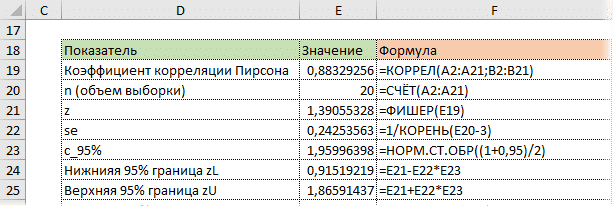
Последний шаг — обратное преобразование Фишера из zar с использованием функции Excel PESCINV. Получаем доверительный интервал коэффициента корреляции.
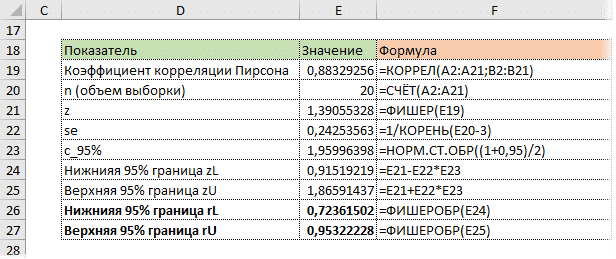
Нижняя граница 95% доверительного интервала коэффициента корреляции — 0,724, верхняя граница — 0,953.
необходимо уточнить, что означает значимая корреляция. Коэффициент корреляции является статистически значимым, если его доверительный интервал не включает 0, то есть истинное значение для генеральной совокупности, вероятно, будет иметь тот же знак, что и оценка выборки.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Выброс может значительно изменить отношения. Поэтому выбросы следует проверять и, при необходимости, удалять перед анализом. Другой вариант — перейти к коэффициенту ранговой корреляции Спирмена. Он также рассчитывается, но не по начальным значениям, а по их рангам (пример показан на видео под статьей).
2. Синонимом корреляции является отношение или ковариация. Следовательно, наличие корреляции (r ≠ 0) не означает причинно-следственной связи между переменными. Возможно, что совместная вариация вызвана влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложной корреляцией.
3. Отсутствие линейной корреляции (r = 0) не означает, что нет никакой связи. Он может быть нелинейным. Частично эта проблема решается с помощью ранговой корреляции Спирмена, которая показывает совместное повышение или понижение рангов, независимо от формы отношений.
На видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, коэффициента ранговой корреляции Спирмена.