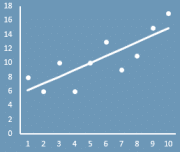
Метод наименьших квадратов — это математическая процедура для построения линейного уравнения, которое наилучшим образом соответствует набору упорядоченных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой. Цель метода наименьших квадратов — минимизировать общую квадратную ошибку между значениями y и. Если для каждой точки определить ошибку ŷ, метод наименьших квадратов минимизирует:
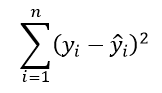
где n = количество пар, отсортированных по строке как можно ближе к данным.
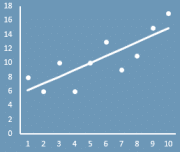
Эта концепция проиллюстрирована на рисунке
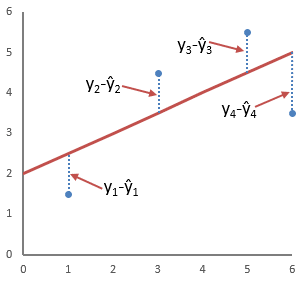
Судя по рисунку, линия, которая ближе всего подходит к данным, линия регрессии, минимизирует общую квадратную ошибку четырех точек на графике. Я покажу вам, как определить это уравнение регрессии с помощью метода наименьших квадратов в примере ниже.
Представьте себе молодую пару, которая недавно жила вместе и делила вместе шкафчик в ванной. Молодой человек стал замечать, что половина его стола неумолимо сжимается, уступая место муссу для волос и соевым комплексам. Последние несколько месяцев парень внимательно следил за тем, как быстро увеличивается количество предметов на его стороне стола. В таблице ниже показано количество предметов, скопившихся у девушки на столе в ванной за последние несколько месяцев.
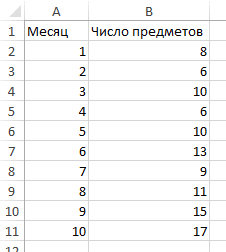
Поскольку наша цель — выяснить, увеличивается ли количество элементов с течением времени, «Месяц» будет независимой переменной, а «Количество элементов» будет зависимой переменной.
Используя метод наименьших квадратов, определите уравнение, которое наилучшим образом соответствует данным, вычислив значения по осям a, y и b, наклон линии:
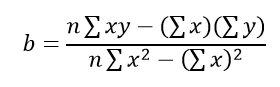
а = yср — bxср
где xav — среднее значение x независимой переменной, yav — среднее значение y независимой переменной.
В следующей таблице приведены расчеты, необходимые для этих уравнений.
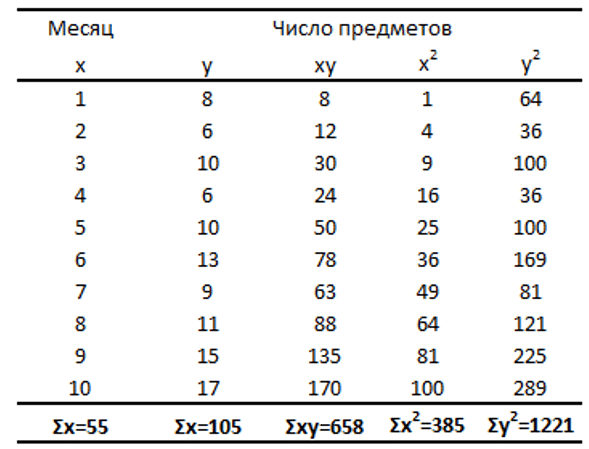
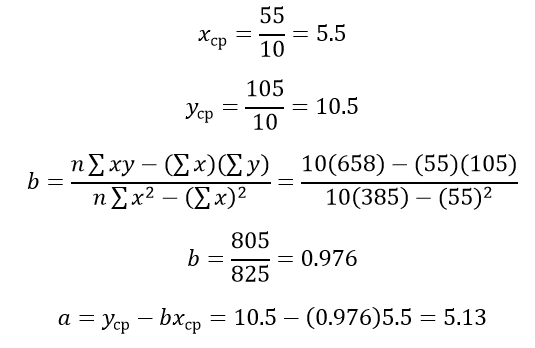
Кривая эффекта для нашего примера с ванной будет определяться следующим уравнением:
= 5,13 + 0,976x
Поскольку наше уравнение имеет положительный наклон 0,976, у мальчика есть доказательство того, что количество элементов в таблице увеличивается со временем в среднем на 1 элемент в месяц. На графике показана кривая эффекта с упорядоченными парами.
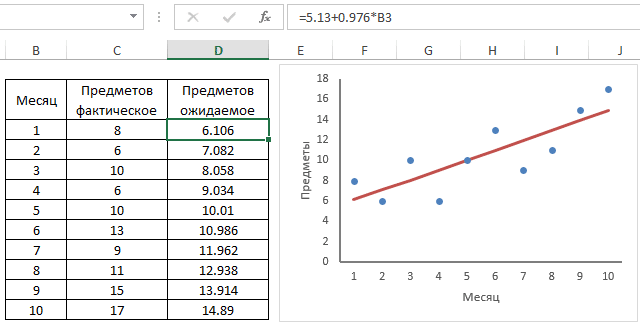
Ожидаемое количество товаров в следующие шесть месяцев (месяц 16) будет рассчитано следующим образом:
ŷ = 5,13 + 0,976x = 5,13 + 0,976 (16) ~ 20,7 = 21 элемент
Итак, пора нашему герою действовать.
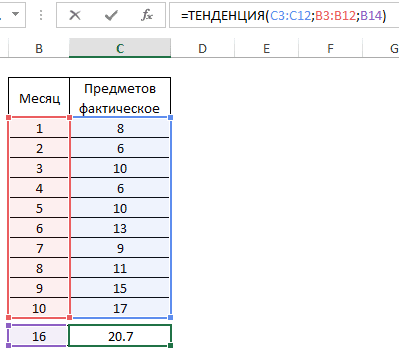
Функция ТЕНДЕНЦИЯ в Excel
Как вы, наверное, уже догадались, в Excel есть функция для вычисления значения методом наименьших квадратов. Эта функция называется ТЕНДЕНЦИЯ. Его синтаксис следующий:
ТЕНДЕНЦИЯ (известные значения Y; известные значения X; новые значения X; const)
где это находится:
известные значения Y — массив зависимых переменных, в нашем случае количество элементов в таблице
известные значения X — массив независимых переменных, в нашем случае это месяц
новые значения X — новые значения X (месяцы), для которых функция ТЕНДЕНЦИЯ возвращает ожидаемое значение зависимых переменных (количество элементов)
const не является обязательным. Логическое значение, указывающее, должна ли константа b быть равна 0.
Например, на графике показана функция ТЕНДЕНЦИЯ, используемая для определения ожидаемого количества предметов на столе в ванной на 16-й месяц.