Сегодня все больше и больше клиентов банка интересуются расчетом максимальной суммы кредита, эффективной процентной ставки, а также поиском формулы для расчета аннуитета и т.д.больше подходит для себя какой-то заем. Кроме того, заранее сделанные самими заемщиками расчеты помогают им при обращении в банк сэкономить много времени, которое им пришлось бы потратить на обход огромного количества финучреждений, а также минимизировать переплату по кредиту. Как вы сами рассчитываете эффективную процентную ставку?
Что нужно для правильного расчета ставки
Итак, вам следует начать с воспоминаний о школьной программе по математике. Затем следует вооружиться калькулятором, бумагой и ручкой. Ну, а тем, кто предпочитает полагаться на компьютер, расчет действительно можно произвести с помощью программы Microsoft Excel. Также нам понадобятся стандартные формулы, которые любят использовать менеджеры банков. И, конечно же, недостаточно написать саму формулу и расшифровать ее буквальный смысл, но и сделать предварительный расчет реальной процентной ставки. Вам также необходимо привести конкретный пример, чтобы вы знали, с чего начать пересчет.
Примеры расчёта
Для наглядности приведем пример из реальной жизни. Клиент банка взял потребительский кредит (потребительский кредит) на сумму 200 000 долларов США на неотложные нужды. Годовая ставка по данному типу банковского кредита составляла 19%, а комиссия банка за использование кредита составляет 2% от общей суммы банковского кредита. При выборе схемы выплат заемщик выбирает размер аннуитета. Таким образом, кредит будет возвращен в течение всего срока кредита, указанного в договоре, равными суммами. Чтобы рассчитать эффективную процентную ставку по кредиту, нам сначала нужно рассчитать сумму платежа по кредиту, которую заемщик будет платить ежемесячно. Воспользуемся формулой расчета аннуитетов, запомните, как она выглядит: A = K * S
- S — общая сумма кредита (в нашем примере она равна S = 200 000);
- K — коэффициент ренты (он напрямую зависит от других значений молей) и рассчитывается по следующей формуле:
Подставляя значения в формулу, получаем: i = 0,016 (19% / 12 месяцев), соответственно n (срок кредита) по нашему примеру 12 месяцев. Затем находим коэффициент аннуитета: K = 0,092252 Следовательно, A = 0,092252 * 200 000, следовательно, A = 18 450,41 доллара.
Способ второй
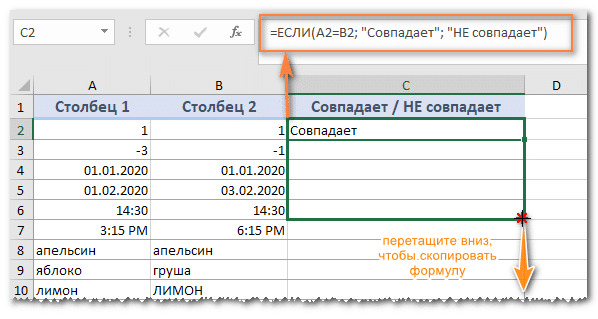
Второй способ расчета ежемесячного платежа по кредиту можно сделать, как указано выше в файле Exel. Для этого в верхнем ряду после fx введите следующие данные: = PMT (0,016; 12; -200000) Благодаря встроенной функции PMT расчет выполняется автоматически. Проверяем наш предыдущий ответ и получаем ту же сумму — 18 450,41 $, что и при расчете по первому способу. После совпадения двух вариантов мы внесем некоторые корректировки и сможем приступить к дальнейшим действиям или составить таблицу месячных зарплат. Пояснения: 0,015 — размер ежемесячной процентной ставки, i = 19.12.100 $ 12 — количество месяцев, входящих в период кредита = n; -200000 — общая сумма кредита = S (пишется со знаком минус). А теперь создадим таблицу:
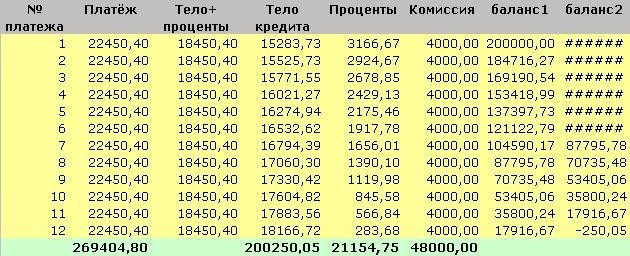
По результатам этой таблицы видно, что каждый месяц количество процентных выплат по кредиту уменьшалось, а выплаты основной части ссуды увеличивались. Это особенность аннуитетной схемы выплаты.
Из представленных в таблице цифр можно сделать следующие выводы:
- Клиент взял ссуду в размере 200 000 долларов США и погасил 269 404,80 долларов США;
- Сумма переплаты по кредиту составила 69 404,80 долларов США;
- И размер процентной ставки увеличился до 34%;
- Ежемесячная плата за пользование кредитом увеличилась с 2% до 48 000 долларов США (выяснилось, что сумма возврата кредита превышает сумму возврата кредита).
В результате сумма превышения во многом связана с ежемесячной оплатой комиссии банка.
