Из-за холодных дней мая и июня 2017 года я изучил климатические данные многолетних наблюдений и хотел опубликовать заметку о статистическом представлении всего этого беспорядка. Чтобы проиллюстрировать одну из своих идей, я построил блок-схему. Во время форматирования я обнаружил, что не совсем понимаю, какие алгоритмы использует Excel для рисования на нем границ квартилей. Углубившись в вопрос, я узнал много нового, чем хотел поделиться с читателями блога. Но мне показалось, что описание тонких алгоритмов висит в воздухе, и поэтому я решил начать с небольшого теоретического введения.
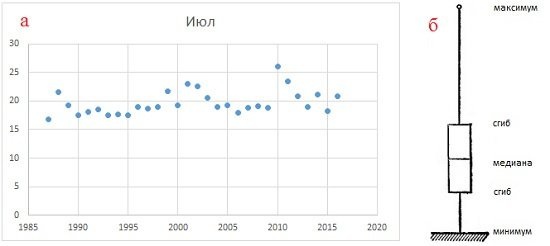
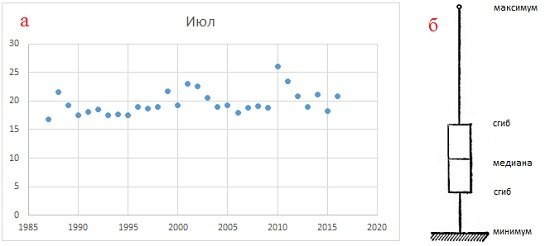
Рис. 1. Визуальное представление образца: (а) диаграмма рассеяния показывает все элементы образца; (б) 5-значное резюме в виде графического поля с усами
5-числовая сводка данных
Изучая выборку, мы можем визуализировать все ее значения (рис. 1а) или научиться выражать наиболее общие общие характеристики в синтетической форме. В последнем случае используются сводки данных. Сегодня наиболее популярными сводками (или статистикой) являются среднее значение и стандартное отклонение (для получения дополнительной информации см. Определение среднего, вариации и формы распределения. Описательная статистика). Однако, во-первых, так было не всегда, и, во-вторых, не во всех случаях эти статистические данные лучше всего описывают выборку.
Интересный пример дает Нассим Николас Талеб (см. Черный лебедь. Под знаком непредсказуемости). Если вы определите средний рост в 100 человек, попадание в число сотен самых высоких людей в мире (2 м 72 см) не сильно изменит средний рост. Но если определить среднее богатство в 100 человек, присутствие среди них Билла Гейтса (86,8 миллиарда долларов) полностью исказит картину. В этих случаях наиболее релевантным итогом является медиана.
Медиана — это такое число, при котором ровно половина выборки больше, а другая половина меньше. Если вы отсортируете случайные данные в порядке возрастания, вы получите несколько вариантов. Если этот ряд содержит нечетное количество элементов, медиана является их средним значением; если даже, то медиана равна половине суммы двух средних элементов.
В его, ставшем теперь классическим, произведении «Анализ результатов наблюдения». Исследовательский анализ Джон Тьюки предлагает 5-значные сводные данные, которые включают: низкий, первый квартиль, медиана, третий квартиль, высокий. Процесс нахождения медианы, а затем квартилей можно представить как складывание листа бумаги. Поэтому Тьюки называет эти новые изогнутые значения (для получения дополнительной информации см. КВАРТИЛЬ: Какие формулы расчета использует Excel). Чтобы визуализировать 5-канальный штифт, Тьюки предлагает нарисовать коробку с усами (рис. 1b).
Диаграмма ящик с усами в Excel 2016
В предыдущих версиях Excel требовалось шаманить для представления статистических данных (см., Например, Биржевую диаграмму, это тоже блочная диаграмма, это тоже прямоугольная диаграмма). Как вариант, я иногда использовал R (см. Алексей Шипунов. Визуальная статистика. Давайте использовать R!). Теперь визуализация статистических данных происходит в несколько кликов. Очень удобно! Но Microsoft по какой-то причине сделала очень краткое описание того, что на самом деле отражают элементы блока, с помощью усовидной диаграммы (см. Поддержка MS). Давайте восполним этот пробел))
На основе данных о средних температурах июля за последние 30 лет (рис. 2) построим диаграмму «ящик-ус).
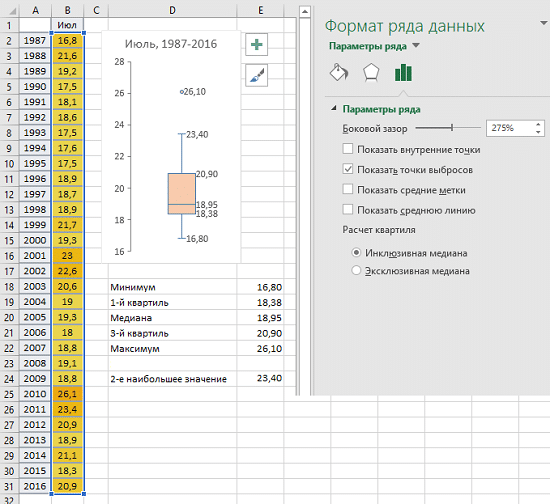
Рис. 2. Основные настройки коробки с усами стол
На рисунке под графиком рассчитана 5-значная сводка. На схеме:
- нижний ус соответствует минимальному значению в выборке данных,
- низ окна — 1-й квартиль,
- линия внутри рамки — это медиана,
- верх коробки — 3-й квартиль,
- верхние усы — до второго максимального значения (выбросы не учитываются); если бы данные не содержали выброса, верхний ус будет соответствовать максимальному значению,
- выбросы могут быть показаны отдельными точками.
Рассмотрим подробнее параметры ряда (см. Формат ряда данных справа на рис. 2). Боковой зазор определяет ширину ящика и ширину горизонтальных краев усов, а также расстояние между ящиками, если их больше (рис. 3). Параметр Show Internal Points говорит сам за себя (рис. 4). Показывать аномальные точки: любопытно, что Excel просто перестает показывать аномальные значения и никак не меняет параметры поля и усов (рис. 5). Показывать средние отметки: вместе со средней линией отражает среднее арифметическое значение для выборки в виде креста (рис. 6). Видно, что среднее арифметическое смещено от медианы вверх (в сторону выброса). Среднее арифметическое более чувствительно к выбросам, чем медиана. Показать среднюю линию — связывает средства разных категорий. Мне не удалось отразить эти строки. И Дмитрий Езипов это сделал.
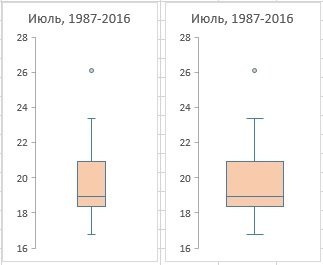
Рис. 3. Боковое пространство: слева — 300%, справа — 100%
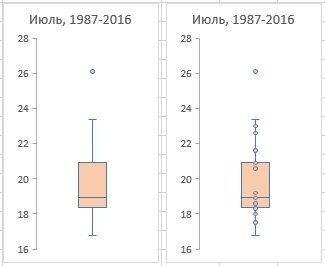
Рис. 4. Показать внутренние точки; слева параметр отключен, справа — включен
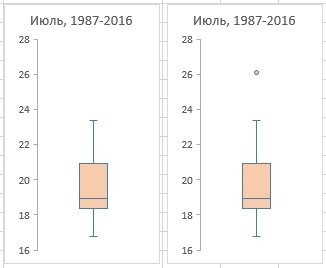
Рис. 5. Показать точки выброса; слева параметр отключен, справа — включен
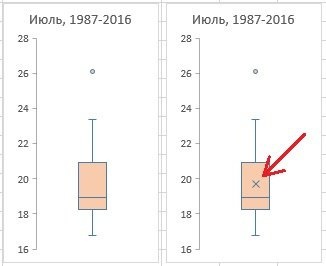
Рис. 6. Показывать средние оценки; слева параметр отключен, справа — включен
Какой метод расчета квартилей предпочесть
И, наконец, самый запутанный вариант форматирования прямоугольной диаграммы и усов-диаграмм — это Quartile Calculator. В сообществе статистиков нет единого мнения по поводу алгоритма расчета квартилей. Excel использует два алгоритма. Если вы хотите понять их полностью, я рекомендую QUARTIL: какие формулы расчета использует Excel. Короче говоря, в Excel есть две функции — КВАРТИЛЬ.EXC () и КВАРТИЛЬ.INC (). Первый использует алгоритм эксклюзивной медианы, второй — включающий. Алгоритм расчета квартилей в первом случае дает значения немного дальше от медианы, т.е прямоугольник немного более вытянут. Вы не можете увидеть это визуально, и только если вы добавите метки данных, цифры покажут этот эффект (рис. 7).
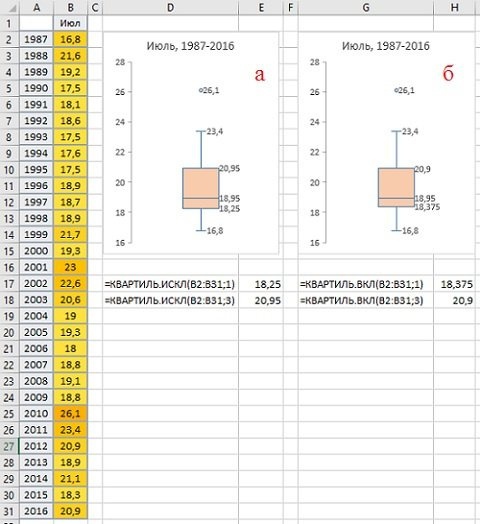
Рис. 7. Расчет квартиля: (а) исключительная медиана, (б) инклюзивная медиана
Если вы обрабатываете данные в разных программах (Excel, R, SAS…), то для совместимости, вероятно, лучше использовать квартили, рассчитанные с использованием метода исключительной медианы. Поскольку этот метод используется во всех продуктах, вы получите одинаковые числа в разных программах. Если вы работаете только в Excel, я бы порекомендовал метод инклюзивной медианы. Он более чувствителен к выбросам, например, при прочих равных условиях QUARTILE.INC () определит точку как выброс с незначительным отклонением от медианы (рис. 8).
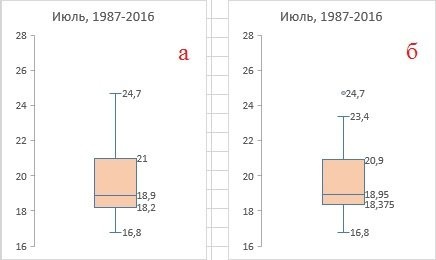
Рис. 8. (b) Точка, идентифицированная функцией QUARTILE.EXC () как выброс, в то время как (a) QUARTILE.EXC () еще не считает эту точку выбросом