Как перевести обыкновенную дробь в смешанную
Для преобразования обыкновенной дроби в смешанную необходимо:
- Разделите числитель на дробь и знаменатель
- Результатом деления будет целая часть
- Остальная часть ветки будет числителем
Сокращение дробей
Дроби можно уменьшить. Сокращение означает, что дробь будет короче и понятнее. Например, дробь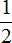 
выглядит намного проще и симпатичнее дроби 
.
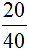Если разрешающая способность примеров оказывается большой и некрасивой дробью, то нужно попробовать ее уменьшить.
Уменьшение дроби основано на основном свойстве дроби. Поэтому, прежде чем изучать редукцию дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется удалением дробей.
Пример 1. Уменьшить дробь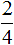 
Итак, вам нужно разделить числитель и знаменатель дроби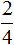 
на наибольший общий делитель 2 и 4.
В этом случае дробь простая и для нее легко найти НОД. НОД чисел 2 и 4 — это число 2. Следовательно, числитель и знаменатель дроби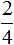 
делится на 2
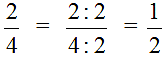
Следовательно, дробь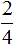 
превращается в более простую дробь 
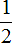… При этом значение исходной дроби не изменилось, так как сокращение подразумевает деление числителя и знаменателя на одно и то же число. И это действие, как было сказано выше, не меняет значения дроби.
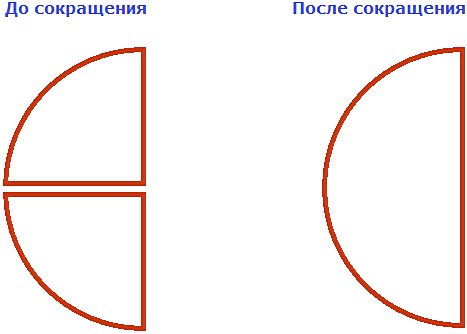
На рисунке показаны дроби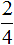 
а также 
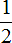в виде кусочков пиццы. До и после резки они одного размера. Единственная разница в том, что делятся они по-разному.
Пример 2. Уменьшаем фракцию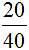 
Чтобы уменьшить фракцию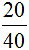 
, необходимо разделить числитель и знаменатель этой дроби на наибольший общий делитель чисел 20 и 40.
Читайте также: Шпаргалка по цветовым схемам — LiveJournal
НОД чисел 20 и 40 — это число 20. Поэтому числитель и знаменатель дроби разделим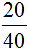 
в 20
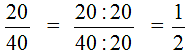
Пример 3. Уменьшаем фракцию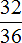 
Чтобы уменьшить фракцию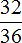 
, разделите числитель и знаменатель этой дроби на наибольший общий делитель 32 и 36.
НОД чисел 32 и 36 — это число 4. Поэтому числитель и знаменатель дроби разделим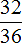 
до 4
См. Также: Все оттенки зеленого: фотография для вдохновения
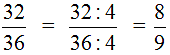
Если в числителе и знаменателе есть простые числа, то дробь не может быть отменена — она не отменяется. Эти дроби называются неприводимыми. Например, неприводимы следующие дроби:
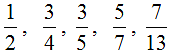
Напомним, что простые числа — это числа, которые делятся только на единицу и сами по себе.
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
Вычитание смешанных чисел
Сначала мы преобразуем смешанные числа в неправильные дроби, затем приводим полученные дроби к общему знаменателю и затем вычитаем друг из друга. Затем выберите всю деталь, если таковая имеется.
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается путем разделения целой части на неправильную дробь. Например, рассмотрим неправильную дробь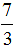 
… Если выделить в нем всю часть, то получится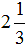 
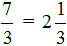
Но возможен и обратный процесс: любое смешанное число можно преобразовать в неправильную дробь. Для этого целую часть нужно умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Результатом будет числитель новой дроби, а знаменатель останется неизменным.
Например, переведем смешанное число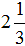 
в неправильной дроби. Умножьте целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем прибавьте числитель дробной части к 6:
6 + 1 = 7
Полученная семерка будет числителем новой дроби, а знаменатель 3 останется неизменным:
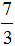
Подробное решение выглядит так:
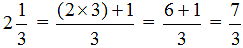
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
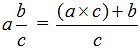
Пример 2. Преобразование смешанного числа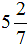 
в неправильной дроби.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем неизменным: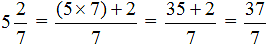 
Деление дробей
Алгоритм деления двух фракций:
- Преобразуйте смешанные дроби в дроби (удалите целую часть).
- Чтобы разделить дроби, вам нужно преобразовать вторую дробь, поменяв местами числитель и знаменатель, а затем умножить дроби.
- Умножьте числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найдите наибольший общий делитель (НОД) числителя и знаменателя и удалите дробь, разделив числитель и знаменатель на НОД.
- Если числитель конечной дроби больше знаменателя, выберите целую часть.
